第三章 灰度变换与空间滤波
背景
灰度变换和空间滤波基础
空间域处理基于表达式
$$
g(x,y)=T[f(x,y)]
$$
其中, $f(x,y)$是输入图像, $g(x,y)$是输出图像, $T$是在点 $(x,y)$的一个领域上定义针对 $f$的算子
灰度变换函数:
$$
s=T(r)
$$
简单起见,使用 $s$或者 $r$ 分别表示$g$和 $f$在任意点 $(x,y)$的灰度
一些基本的灰度变换函数
图像反转
灰度级在区间 $[0,L-1]$的反转图像形式为
$$
s = L-1-r
$$
使用这种方式反转图像的灰度级,会有一种类似于照片底片的结果。
可用于增强图像暗色区域的白色或者灰色细节,若暗色区域的尺寸很大这种增强效果会更好
对数变换
对数变换的通式为
$$
s = clog(1+r)
$$
c是一个常数,并且 $r\geq0 $
此变换会将输入中范围较窄的低灰度值映射为输出中范围较宽的灰度级,输入中的高灰度值则会被映射为输出中范围较窄的灰度级,使用此方法来扩展图像中的暗像素值。反对数变换的作用与此相反
幂律(伽马)变换
通过压缩或者扩展图像的灰度级来增强图像对比度
表达式为:
$$
s=cr^\gamma
$$
其中$c$ 和 $\gamma$ 均为正常数,若考虑到偏移情况,即输入为0的时候的一个可度量输出,有时公式也会为:$s=c(r+\epsilon)^\gamma$但偏移往往会是校准问题,因此可忽略不计
分段线性变换函数
与前面函数相比的优点为:其形式可以任意复杂;缺点是会要求用户输入很多参数。
对比度拉伸
通过扩展图像的灰度级范围,使其覆盖记录介质或者显示设备的整个理想灰度范围
灰度级分层:突出图像中特定灰度范围的亮度
突出图像的特定灰度区间,有如下两种基本方法的变体:
- 将感兴趣范围内所有的灰度值显示为一个值(如白色),其他灰度值显示另外一个值(如黑色),产生一幅二值图像
- 使期望的灰度范围变亮(或变暗),但保持图像的其他灰度级不变
比特平面分层
像素值是由比特组成的整数。如在256级灰度图像中,图像值是由8比特组成的,其中平面1包含图像中所有像素的最低有效比特,平面8则包含所有像素最高有效比特。
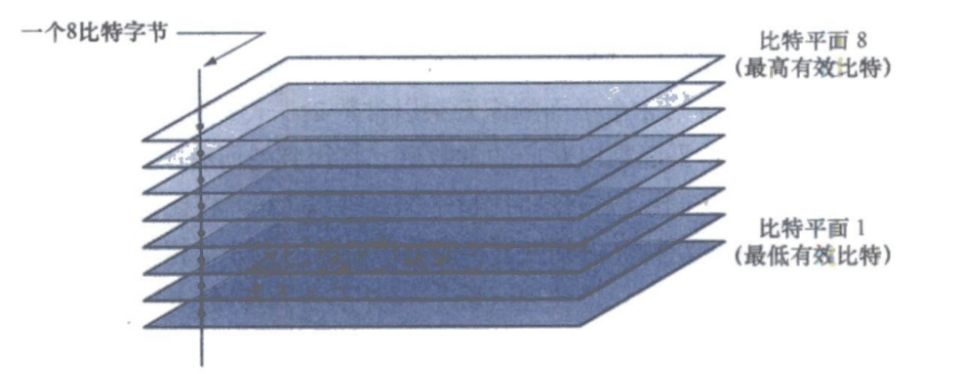
将图像分解成各个比特平面对分析图像每个比特的相对重要性使有用的,可以确定量化图像所用比特的充分性。
突出特定比特。四个高阶比特平面包含视觉上重要的大多数数据,低阶比特平面贡献了更精细的灰度细节。原图像中任意一个像素的值可以由比特平面中对应的二进制像素值来重建,可以用于减少存储量
直方图处理
令 $r_k , k=0,1,2,……,L-1$表示一副 $L$级回复数字图像 $f(x,y)$的灰度。 $f$的非归一化直方图定义为
$$
h(r_k)=n_k \ \ \ \ k=0,1,2,……,L-1
$$
其中, $n_k$是 $f$中灰度为 $r_k$的像素的数量。类似的, $f$的归一化直方图定义为
$$
p(r_k) = \frac{h(r_k)}{MN} = \frac{n_k}{MN}
$$
其中, MN分别是图像的行和列。多数情况下处理的是归一化直方图,简称为直方图或者图像直方图
若像素占据整个灰度级范围并且均匀分布的图像,将具有高对比度的外观和多种灰色调。
直方图基本灰度特征
Q:直方图相同的图像,是否为同一个图像?
A:是同一个图像
四个直方图灰度级特征
暗图像
大多数直方图容器集中在灰度级比较低的区域
亮图像
大多数直方图容器集中在灰度级的高端
低对比度图像
直方图容器基本位于灰度级的中间,对于单色图像来讲,意味着暗淡的灰色外观
高对比度的图像
直方图容器覆盖了较宽的灰度级,并且像素分布较为均匀,容器高度基本相同
图片如下:
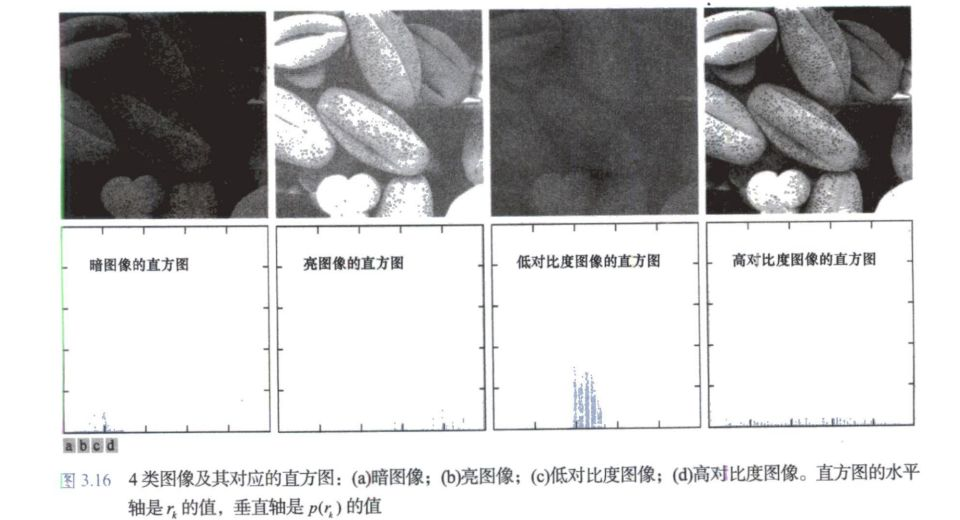
直觉上,我们可以得到如下内容:
像素占据整个灰度级范围并且均匀分布的图像,将具有高对比度的外观和多种灰色调
累计直方图CDF

直方图均衡化【相关知识点:书P87】
假设灰度值最初是连续的,令变量 $r$表示待处理的图像灰度。 $r \in [0,L-1]$ , $r=0$表示黑色, $r=L-1$表示白色。对于这些满足条件的 r,重点关注如下形式的灰度映射:
$$
s = T(r), \ \ \ 0\leq r \leq L-1
$$
题目1
一幅大小为(64*64)的灰度图像,共有8个灰度级,其灰度级分布见下表,现要求对其进行均衡化处理
| 序号 | 运算 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 列出原始灰度级f | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 列出原始直方图 | 0.12 | 0.01 | 0.14 | 0.09 | 0.44 | 0.09 | 0.08 | 0.03 |
| 3 | 累计直方图 | 0.12 | 0.13 | 0.27 | 0.36 | 0.8 | 0.89 | 0.97 | 1 |
| 4 | 累计直方图*7 | 0.84 | 0.91 | 1.89 | 2.52 | 5.6 | 6.23 | 6.79 | 7 |
| 4 | 四舍五入取整g | 1 | 1 | 2 | 3 | 6 | 6 | 7 | 7 |
| 5 | 确定映射关系f->g | 0->1 | 1->1 | 2->2 | 3->3 | 4->6 | 5->6 | 6->7 | 7->7 |
| 6 | 新直方图$n_k/n$ | 0 | 0.13 | 0.14 | 0.09 | 0 | 0 | 0.53 | 0.11 |
解题思路:
累计直方图:其为原始直方图相加得到:列出原始直方图 0.12 0.01 0.14 0.09 0.44 0.09 0.08 0.03 累计直方图 0.12 0.12+0.01 0.12+0.01+0.14 0.12+0.0.1+0.14+0.09 …… …… …… 1 累计直方图*7:其为累计直方图值*7所得:累计直方图 0.12 0.13 0.27 0.36 0.8 0.89 0.97 1 累计直方图*7 0.12*7 0.13*7 …… …… …… …… …… 7 四舍五入取整g:其为对累计直方图*7进行取整可得:累计直方图*7 0.84 0.91 1.89 2.52 5.6 6.23 6.79 7 四舍五入取整g 1 1 2 3 6 6 7 7 确定映射关系f->g:则是对获得的g与最开始的列出原始灰度级f进行比较,看其与哪一个值进行对应:列出原始灰度级f 0 1 2 3 4 5 6 7 四舍五入取整g 1 1 2 3 6 6 7 7 确定映射关系f->g 0->1 1->1 2->2 3->3 4->6 5->6 6->7 7->7 新直方图$n_k/n$:便是将所对应的映射关系进行对应的原始直方图数据进行重合累加:
列出原始灰度级f 0 1 2 3 4 5 6 7 列出原始直方图 0.12 0.01 0.14 0.09 0.44 0.09 0.08 0.03 确定映射关系f->g 0->1 1->1 2->2 3->3 4->6 5->6 6->7 7->7 新直方图$n_k/n$ 0 0.12+0.01 0.14 0.09 0 0 0.44+0.09 0.08+0.03
至此题目做完。
直方图匹配化(规定化)【相关知识点书P92】
题目1
一幅大小为(64*64)的灰度图像,共有8个灰度级,其灰度级分布见下表,现要求对其按照给定的图像r的直方图进行匹配化处理
| 序号 | 运算 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 列出原始灰度级f | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 列出原始直方图PDF(f) | 0.12 | 0.01 | 0.14 | 0.09 | 0.44 | 0.09 | 0.08 | 0.03 |
| 3 | 原始图像的累计直方图CDF(f) | 0.12 | 0.13 | 0.27 | 0.36 | 0.8 | 0.89 | 0.97 | 1 |
| 4 | 原始图像的累计直方图*7 | 0.84 | 0.91 | 1.89 | 2.52 | 5.6 | 6.23 | 6.79 | 7 |
| 5 | 原始图像的累计直方图四舍五入取整g | 1 | 1 | 2 | 3 | 6 | 6 | 7 | 7 |
| 6 | 参考直方图PDF(r) | 0 | 0 | 0 | 0.15 | 0.2 | 0.45 | 0.2 | 0 |
| 7 | 参考直方图CDF(r) | 0 | 0 | 0 | 0.15 | 0.35 | 0.8 | 1 | 1 |
| 8 | 参考直方图CDF(r)*7 | 0 | 0 | 0 | 1.05 | 2.45 | 5.6 | 7 | 7 |
| 9 | 参考直方图CDF(r)*7,四舍五入取整 | 0 | 0 | 0 | 1 | 2 | 6 | 7 | 7 |
| 10 | 完成规定化需要的映射 | 0-3 | 1-3 | 2-4 | 3-4 | 4-5 | 5-5 | 6-6 | 7-6 |
| 11 | 新直方图 | 0 | 0 | 0 | 0.13 | 0.23 | 0.53 | 0.11 | 0 |
解题思路:
序号1-9与上文基本一样,因此不在赘述;
完成规定化需要的映射:将原始图像的累计直方图四舍五入取整g与参考直方图CDF(r)*7,四舍五入取整进行对比,如果不存在一一对应关系则就近划分,将后续比对的值与列出原始灰度级f进行对应,即:列出原始灰度级f 0 1 2 3 4 5 6 7 原始图像的累计直方图四舍五入取整g 1 1 2 3 6 6 7 7 参考直方图CDF(r)*7,四舍五入取整 0 0 0 1 2 6 7 7 完成规定化需要的映射 0-3 1-3 2-4 3-4 4-5 5-5 6-6 7-6

后续操作与上文一致,不在进行过多赘述。
空间滤波基础
滤波:通过、修改或者抑制图像的规定频率分量。例如通过低频的滤波器为低通滤波器(模糊图像来平滑图像),可以直接对图像本身进行类似平滑处理。使用空间滤波器可以直接对图像本身进行类似的平滑处理。
空间滤波将每个像素值替换该像素何其邻域的函数值来修改图像。若是线性的,则为线性空间滤波器,否则为非线性滤波器
线性空间滤波原理
线性空间滤波器在图像 $f$和滤波器核 $w$之间执行乘积之和运算,其中核是一个阵列,其大小代表了需要运算的邻域大小,其系数决定着该滤波器的性质。
下图是以 $3*3$核进行线性空间滤波的原理:
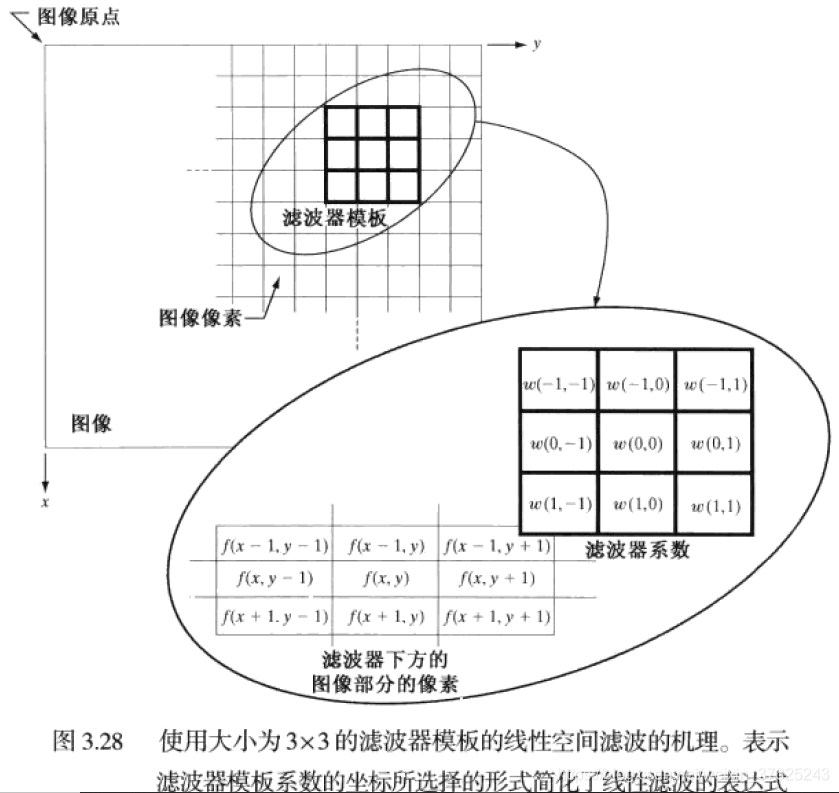
一般来讲,大小为 $mn$的核对应大小为 $MN$的图像的线性空间滤波器可以表示为:
$$
g(x,y) = \sum_{s=-a}^a \sum_{t=-b}^b w(s,t)f(x+s,y+t)
$$
空间相关与卷积
相关
滤波器模板移过图像并计算每个位置的乘积之和
单位离散冲激
包含一个
1而其余项都是0的函数
卷积
预先将滤波器旋转180°,执行与相关相同的滑动乘积求和操作

下面的内容直接给出公式,详情解释在第四版教材的P104-P105
冲激
坐标 $(x_0,y_0)$处的离散冲激强度(振幅)A 定义为:
$$
\delta(x-x_0,y-y_0)=\begin{cases}A,x_0=x 和 y_0 =y\0,其他\end{cases}
$$卷积相关
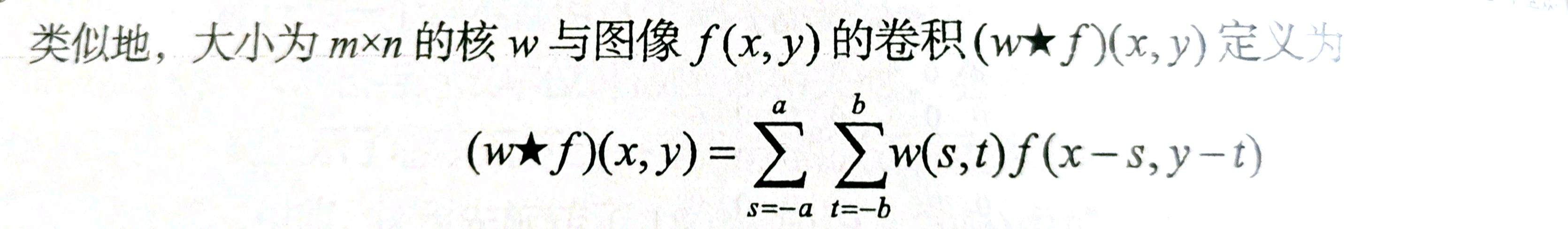

空间域滤波和频率域滤波的一些重要比较
- 卷积是空间域滤波的基础,它等效于频率域中的乘法,反之亦然
- 空间域中振幅为A的冲激,是频率域中值为A的一个常数,反之亦然
如何构建空间滤波器核
有三种方法可以对其进行构建
根据数学性质
计算邻域平均值滤波器会模糊图像,计算平均值会类似于积分;计算图像局部导数的滤波器会锐化图像
对形状具有所需性质的二维空间函数进行取样
使用高斯函数样本可以构建加权平均滤波器
设计具有规定频率响应的空间滤波器
数字滤波器设计范畴
平滑(低通空间滤波器)
用于降低灰度的极具过渡,由于随机噪声通常由灰度的极具过渡组成,因此其最明显的一个应用便是降噪。
- 应用
- 减少图像之间的无关细节
- 平滑因灰度级数量级不足导致的伪轮廓
盒式滤波器
最简单的可分离低通滤波器核是盒式核,其系数通常相同(通常为1)下图为一个大小为3*3的盒式滤波器
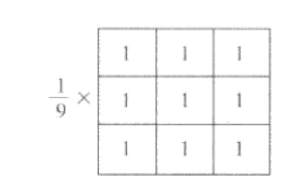
一般来讲,其前面有一个归1化的系数,其值为1除以系数值之和(当所有系数为1时,值为 $1/mn$),有两个目的:
- 一个恒定灰度区域的灰度平均值将等于滤波后的图像灰度值
- 采用这种方式归一化之后,可防止在滤波过程中引入偏差
低通高斯滤波器核
有待添加
统计排序(非线性)滤波器
以滤波器包围的图像区域中所包含的像素的排序为基础,使用统计排序结果决定的值代替中心像素的值
中值滤波器,将像素邻域内灰度的中值代替该像素的值,比相同尺寸的线性平滑滤波器的模糊程度低,对处理脉冲噪声(椒盐噪声)非常有效。主要功能是使拥有不同灰度的点看起来更接近其相邻点,用于去除相对于其邻域像素更亮或更暗且其区域小于 $m^2/2$(滤波器区域的一半)的孤立像素族
其为目前数字图像处理最有用的统计排序滤波器
锐化(高通)空间滤波器
锐化作用时突出灰度中的过渡,
平滑通常为低通滤波,锐化通常为高通滤波
作用:
- 突出灰度的过渡部分,可由空间微分实现
- 微分算子的响应程度与图像在用算子操作这一点的突变成正比
- 图像微分增强边缘和其他突变(如噪声),削弱灰度变换缓慢的区域
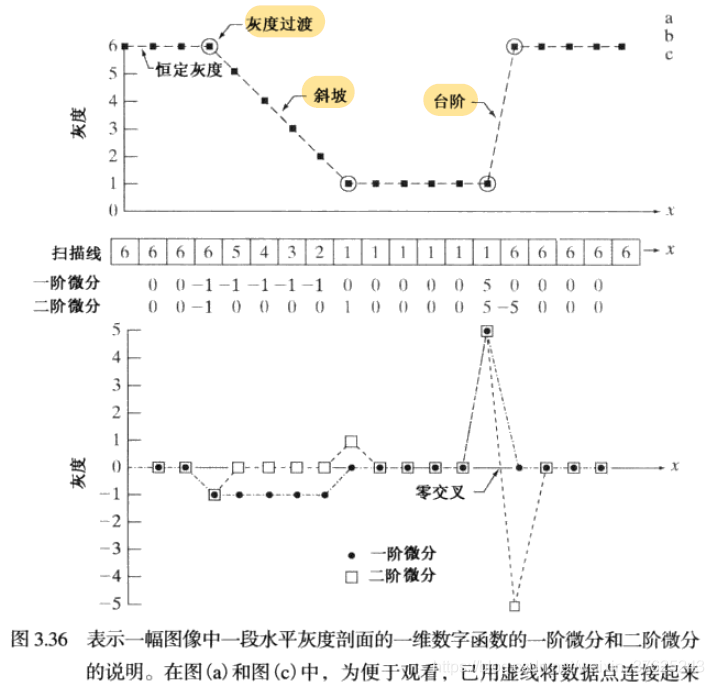
使用二阶微分进行图像锐化——拉普拉斯
定义一个二阶微分的离散公式,并基于此构造一个基于该公式的滤波器模板
最简单的各项同性微分算子是线性的
二维图像函数 $f(x,y)$的拉普拉斯算子定义:
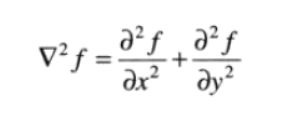

因此,其对应的滤波模板为:
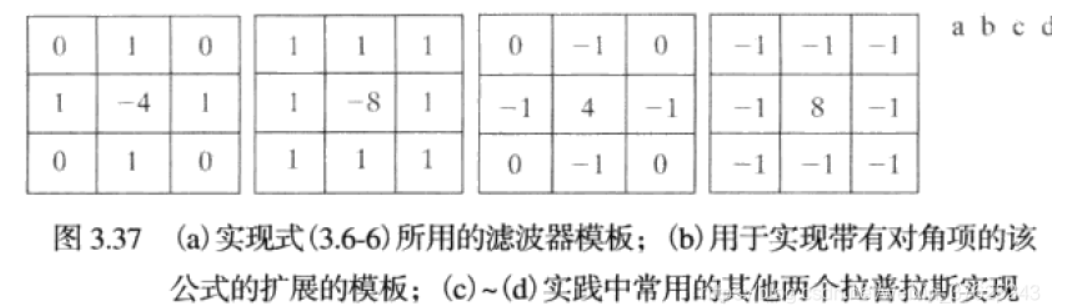
使用拉普拉斯算子对图像增强的基本方法

强调图像中灰度的突变,不强调灰度级缓慢变换的区域
由于在拉普拉斯图像中既有正值,又有负值,并且所有负值在显示时都修剪成0,所以图像大多都是黑色的
一个典型的标定拉普拉斯图像的方法是对其最小值加一个新的0代替最小值,然后将结果标定到整个灰度范围$[0-L-1]$中
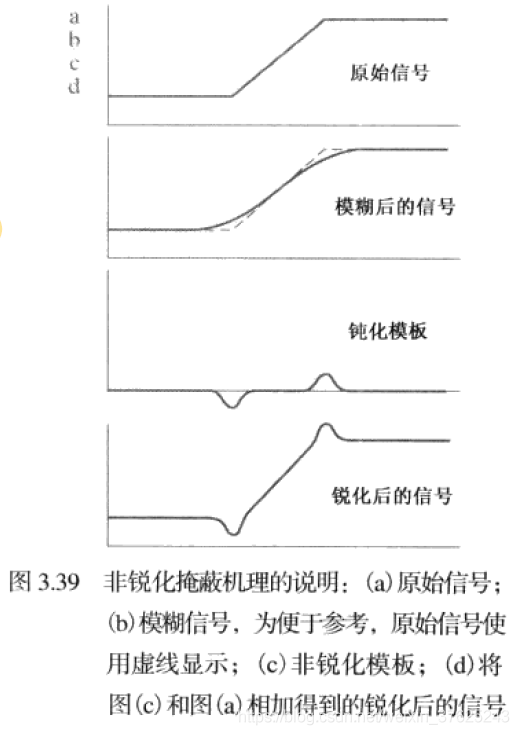
钝化掩蔽和高提升滤波
从原图像中减去一幅非锐化(平滑过的)版本
步骤如下:
- 模糊原图像
- 从原图像中减去模糊图像(产生的差值图像称为模板)
- 将模板加到原图像上

如上图所示,式中包含一个权值$K,k\geq 0$
- 当$k=1$时,为钝化掩蔽
- 当 $k>1$时,这个过程为高提升滤波
- 若选择 $k<1$时可以减少钝化模板的贡献
钝化掩蔽原理如下图所示,其:
- 强调了锐化后信号中出现灰度斜率变换的点
- 如果原图像有任何零值,或如果选择的k值大到足以使模板峰值大于原信号中的最小值时,最终的结果可能会存在负灰度。
- 负值将导致边缘周围有暗的晕轮。如果k足够大,将产生不好的结果。
使用一阶导数锐化图像——梯度
图像 $f$在 $(x,y)$中的梯度被定义为二维列向量,其重要几何性质为指向了 $f$最大变换率的方向
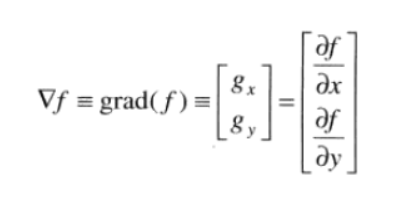
其中,

以下的两个3*3的算子为 slobe算子(如下图),其中心系数为2是通过突出中心点来进行平滑处理,其所有核系数均为0,表明其灰度恒定区域的响应为0,因此可用于边缘增强

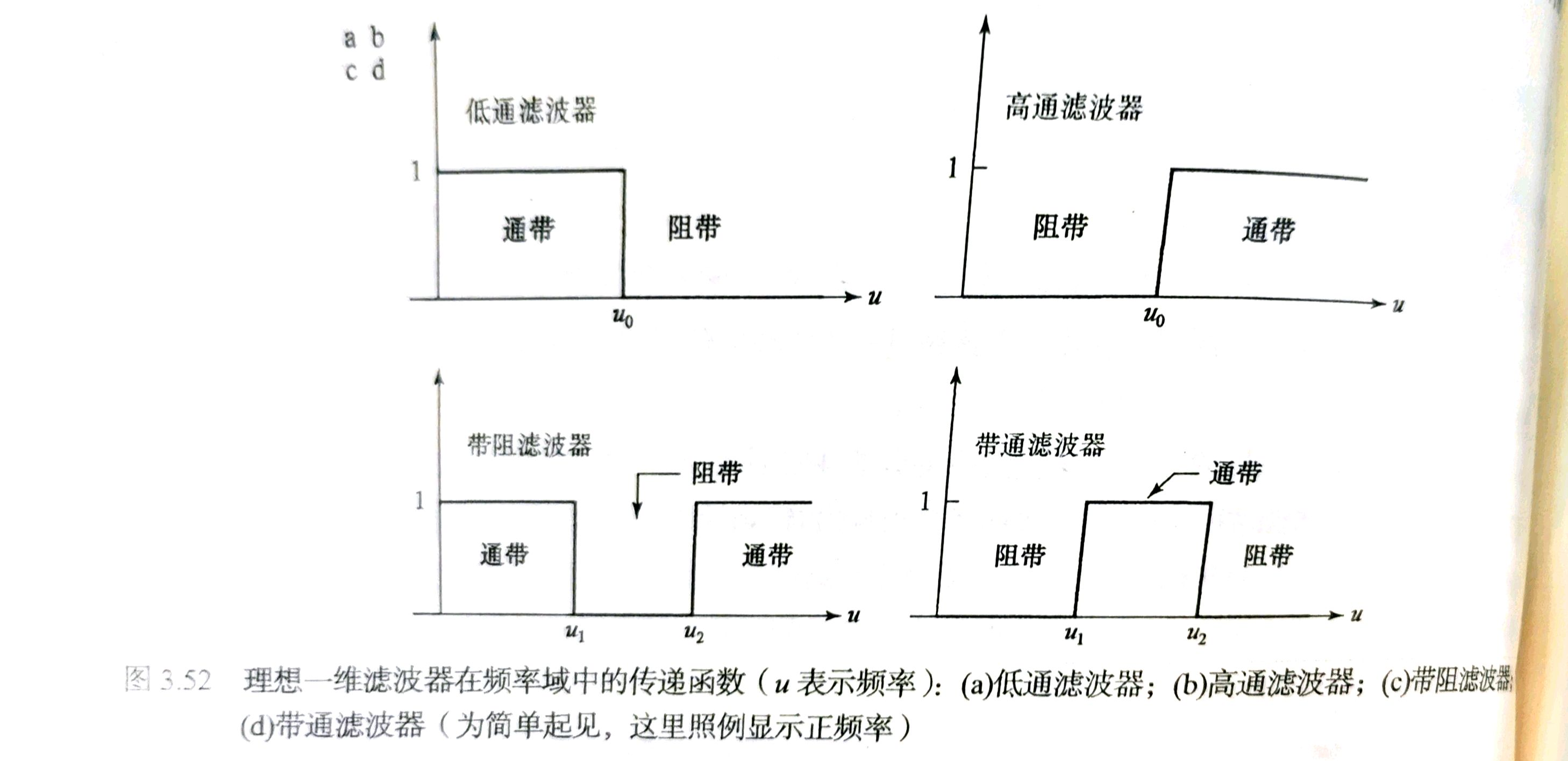
低通、高通、带阻和带通滤波器
其传递函数如下图所示:
其所对应的相关空间核如下图所示:

组合使用空间增强方法
将多种图像增强方法结合起来,完成图像增强任务