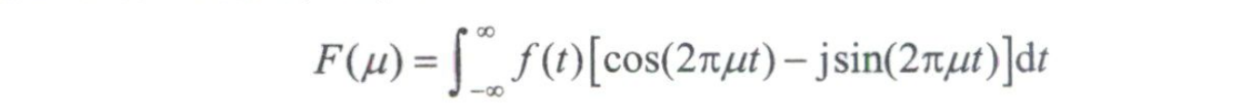频率域滤波
基本概念
复数
复数的定义为:
$$
C = R+jI
$$
其共轭复数为:
$$
C^* = R-jI
$$
傅里叶级数
具有周期T的连续变量t的函数f(t)可被描述为乘以适当系数的正弦和/或余弦和
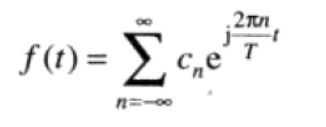
其中,系数 $C_n$为:
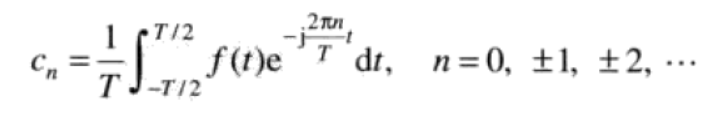
冲激函数及其取样(筛选)性质
连续变量$t$在$t=0$处的单位冲激为$\delta (t)$,定义如下,且满足第二个式子。物理上把t看成时间,则一个冲激可理解为幅度无限、持续时间为0,拥有单位面积的尖峰信号
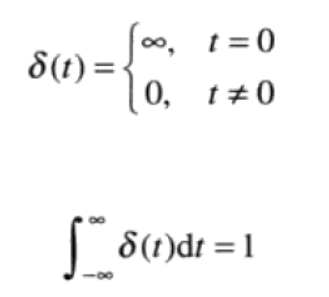
其中,若将t解释为时间时,冲激就可以被是为幅度无限、持续时间为0,并且具有单位面积的尖峰信号。其具有关于积分的取样性质:
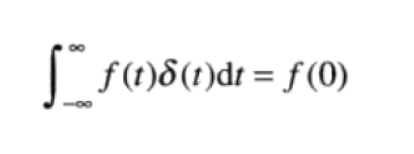
若假设, $f(t)$在 $t=0$处是连续的,位于任意一点的 $t_0$的冲激表示为 $ \delta(t-t_0)$,取样特性在冲激位置 $t_0$处得到函数值
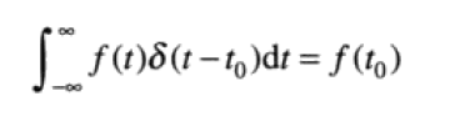
离散形式:

冲击串:无穷多个冲激 $\Delta T$的单位之和

连续单变量函数的傅里叶变换

其中,式(4.20)与式(4.21)共同构成傅里叶变换对,通常表示为:$f(t)\Leftrightarrow F(\mu)$
根据相关公式,我们可以将式(4.20)改写成为