国考之资料分析
前言
在此处记录一下资料分析的相关知识点,内容来自于花生十三
在花生十三这里,有几个数据需要记录:
- B:现期值
- A:基期值
- R:增长率
- X:增长量
四则运算
高位叠加
与记忆中的列竖式作加法顺序相反,高位叠加是从高位加起,抓住问题的主要矛盾。非精确求和和没有选项可以参考时可以使用高位叠加
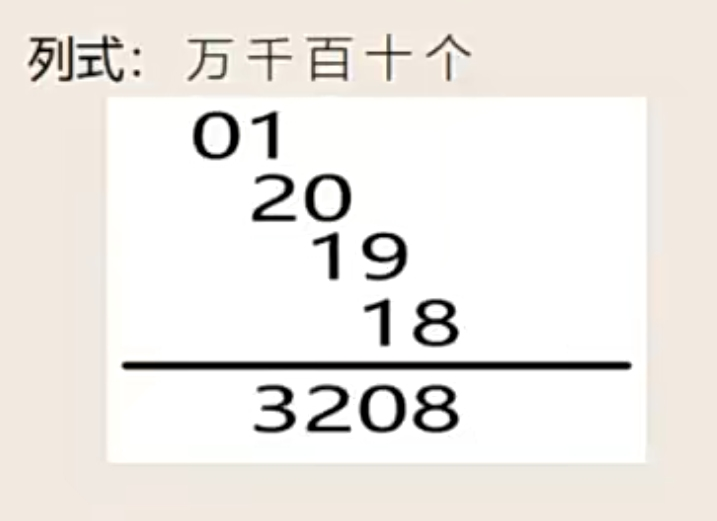
适合:非精确题目
适用范围:求比重、合计多少、
“21” “12”分段法
将三位数的减法分为“21”或者“12”两段,并尽可能保证不需要借位
如 519-127:
个位:9>7,百位+十位:51>12;我们可以将减法进行分段计算,百位+十位为一段“2”,个位为一段“1”
则个位 = 9-7=2;百位+十位 = 51-12=39;将数据回归原位,答案=392
整数基准值法
被减数-减数=(被减数-基准值)+(基准值-减数)
如 632-588 :
十位+个位中的3 2均小于 8 8;因此可以加入基准值,将减数588向上取整为600,则
$$
632-588 = (632-600)+(600-588) = 44
$$
小分互换
若乘法中有某个乘数可以近似转化为某个常见分数,我们可以将多位数乘法转华为简单的除法计算
常见百化分分数:
| 1/2 = 50% | 1/7=14.3% | 1/12=8.3% | 1/17=5.9% |
|---|---|---|---|
| 1/3=33.3% | 1/8=12.5% | 1/13=7.7% | 1/18=5.6% |
| 1/4=25% | 1/9=11.1% | 1/14=7.1% | 1/19=5.3% |
| 1/5=20% | 1/10=10% | 1/15=6.7% | 2/7=28.6% |
| 1/6=16.7% | 1/11=9.9% | 1/16=6.3% | 3/7=42.9% |
如 464*25% :
$$
25%=1/4,则46425%=464/4=116
$$
如果遇到不是那么整的数值,如$46412.1%$,则可以考虑将$12.1%化为11.1%+1%$之后转成$\frac{464}{9}+4.64\approx56.2$
凑整拆分
将乘数拆分为“2或5”等容易计算的数字组成
如 464*48%:
$$
46448% = 464(50%-2%) = 464/2-464*2% =232-9.28=222.72
$$
预估拆分法
将被除数由大到小拆成几部分分别计算,通过逐步分解,从而得到结果。
例1:
$\frac{715}{729} = \frac{729-14}{729}=1-\frac{14}{729}\ \ \ \ 由于,\frac{14}{729} =2^-%,\ \ \ \ 因此\frac{715}{729} = 98^+%$
例2:
$\frac{247}{532}=\frac{266-19}{532}=50%-4^-%=46^+%$
例3:
$\frac{335}{831}\ \ 大体可以看出,约40%,因此40%*831=332,\frac{335}{831}=\frac{332+3}{831}=40%+0.4^-%=40.4^-%$
使用规则:
- 如果分数大小接近1(分子分母相差不大)可以先用100%减去、加上
- 如果分子在分母的50%附近,先拆出50%
- 如果分子在分母的50%-100%之间且不好预估,先拆出50%,之后继续计算
- 如果分母接近500或1000,可以直接根据分子判断分数大约的百分比
- 在不满足上述情况下,可以根据首位比值或分子前两位与分母首位比值,拆出其它特殊分数(如:1/3、1/4、1/6、1/7、30%、40%、70%等)
“415”份数法
将数量关系转化为份数比例关系,从而简化计算。一般来讲,将现期B和增长率R为已知量的前提下,可以使用415份数法快速获得基期A与变化量X的数值
例如:增长率为25%($\frac14$),为了方便计算,可以将基期设为4份,变化量X=AR=1份,现期为基期和变化量之和,为5份。则基期、变化量、现期的份数分别为4、1、5
使用时机:增长率R在一个分数附近
例:
今年工资456,比去年降低了12.5%,则去年工资是多少?
$-12.5%=-\frac18$,则对于“415”份数来讲,现期为7份,增长量为-1份,基期为8份,$\frac{456}{7} \approx65$,则基期为“7+1”则为$65+456=521$
假设分配法
现期、基期、增长量成一定比例,且现期=基期+增长量,通常通过假设基期、增长量来分配现期,多退少补,逐步趋于正确的基期和增长量。
核心公式:
- B=A+X——剩余分配=B-A-X
- A=B/(1+R)——A:X:B=x:100:100+x
- X=AR
- R>0——ABX同号,且A<B
- R<0——AB与X异号,且A>B
其结构图大致如下:
1 | graph TB |
左边分支为基期值,右边分支为增长量,中间剩余分配值为基期值与增长量和现期的差(基期和增长量的数值为假定)
由于大部分情况下知道现期、增长量的值,求基期的情况较多,因此,以下为两个例子
例1(0<x<10%):
假设现期量为5362,增长了8%,求基期or增长量:
假设基期量为5000,其8%为400,5000+400=5400,与5362相差38,因此中间位置写-38,两侧分别写5000和400,之后将-38看作-40,以40*8%=3%,填入右侧,则左侧值为38-3=35。因此基期值为4965,增长量为397
1 | graph TB |
例2(x>10%):
假设现期量为402,增长了16%,求基期or增长量:
假设基期量为300,其增长量为300*16%=48,因此可以得到剩余量为402-300-48=54,由于增长量为16%,近似约等于可以看成16.7%,为$\frac16$,则增长一份的量为$\frac{54}{7}\approx8$,则增长量为8,基期量为46。因此基期为346,增长量为56
1 | graph TB |
在第二步的时候使用“415”方法,第一步使用误差较大,可能会导致无法选择合适数据
例3(x<0):
假设现期量为456,减少了7%,求基期or增长量:
假设基期量为500,则增长量为-35,剩余量为456-500-35=-9,之后使用-9*-7%可以得到约等于1,则前面为-10
1 | graph TB |