第二章 数字图像基础
人眼的结构
光感受器
分为锥状体和杆状体
锥状体
600-700万个,主要分布在视网膜中央凹的中间部分,对颜色高度敏感,每个锥状体都连接到了自身的神经末梢,锥状体视觉被称为明视觉或者亮视觉
7500-15000万个,分布面积大,并且几个杆状体连接一个神经末梢,捕获视野内整体图像,没有色觉,对低光照度敏感,暗视觉或微光视觉
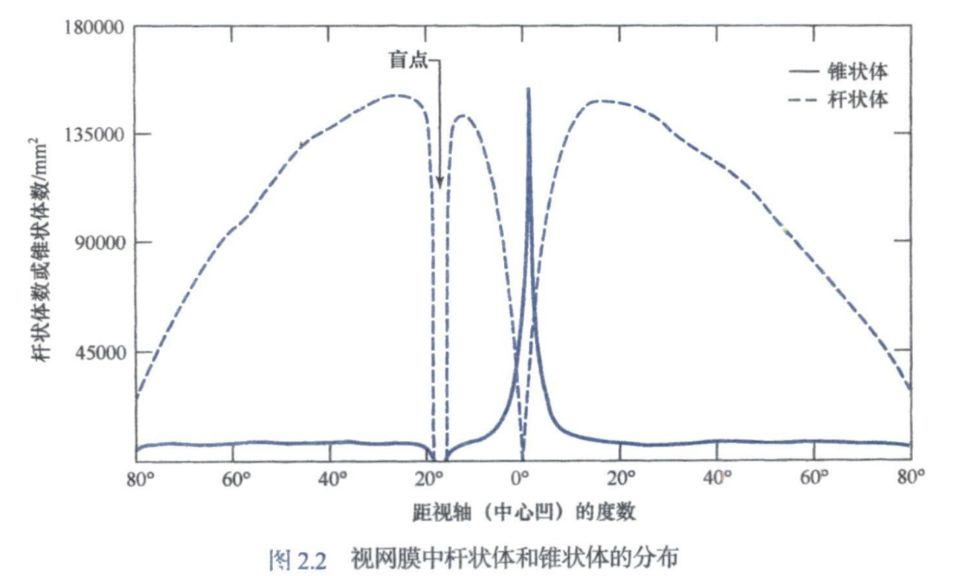
人眼图像的形成
晶状体和成 像区域(视网膜)之间的距离是固定的,正确聚焦的焦距是通过改变晶状体的形状得到的。在远离或 接近目标时’睫状体中的纤维通过分别压扁或加厚晶状体来实现聚焦
视网膜图像主要聚焦在中央凹区域。然后’光感受器的相对激励作用产生感知,把辐射能量转换为最终由大脑解码的电脉冲
亮度适应和识别
- 两种现象表明感知亮度不是实际灰度的简单函数
- “上冲”或“下冲”现象——又称马赫带效应
- 同时对比:一个区域的感知亮度并不只是取决于其灰度
图像获取及感知
常用成像传感器配置有哪些
- 单个成像传感器
- 条带传感器
- 阵列传感器
成像原理
组合输入电能和传感器对正被检测能量类型的响应,将入射能量转换为电压
一个简单的成像模型
用形如 $f(x,y)$的二维函数来表示图像。在空间坐标(x,y)处的 $f$的值是一个标量,其物理意义由图像源决定,其值与物理源辐射的能量成正比。因此 $f(x,y)$值一定非负的和有限的,即
$$
0\leq f(x,y)<∞
$$
函数 $f(x,y)$由两个分量表示:1. 入射到被观察场景的光源照射量 2. 被场景中物体反射的照射量 被称为入射分量和反射分量,并用 $i(x,y)$与 $r(x,y)$进行表示。这两个函数的乘积形成 $f(x,y)$即
$$
f(x,y) = i(x,y)r(x,y)
$$
其中 $0\leq i(x,y) <∞$ , $0\leq r(x,y)\leq1$
于是,反射分量被限制在0(全吸收)和1(全反射)之间。 $i(x,y)$的性质取决于照射源,而 $r(x,y)$的性质取决于被成像物体的特性。
图像取样以及量化
取样和量化的基本概念
对坐标值进行数字化称为取样,对幅度值进行数字化称为量化
灰度分辨率
指在灰度级中可分辨的最小变化
最常用是8bit,还有16bit,32nit
通常是量化灰度时所用的比特数
灰度被量化为256级的图像,灰度分辨率为8bit
伪轮廓
恒定灰度区域内有一组不易察觉的精细脊状结构,因为数字图像平滑区域中的灰度级不足引起的
对比度
一幅图像中最高和最低灰度级间的灰度差。当图像中像素可感知的数值有高的动态范围时,认为该图像有高的对比度
图像内插
在图像放大、缩小、旋转和几何校正等任务中使用
内插是用已知数据来估计未知位置的值的过程
最邻近内插
将原图像中最邻近的灰度赋给每个新位置
方法简单,但是会产生人为失真(直边失真)
双线性内插
使用四个最邻近的灰度来计算给定位置的灰度。令 (x,y)表示待赋灰度值的位置的坐标,令 $v(x,y)$表示灰度值。所赋值由如下公式可得:
$$
v(x,y) =ax+by+cxy+d
$$
4个系数可用点(x,y)的4个最邻近点写出的4个未知方程求出结果比最邻近要好,但计算量大
双三次内插
包括16个最邻近点。赋给点(x,y)的灰度值由如下公式得到:
$$
v(x,y) = \sum_{i=1}^3 \sum_{j=0}^3 a_{ij}x^iy^j
$$
其中,式子中16个系数可用点(x,y)的16个最近临点写出的16个未知方程求出保留细节方面强于双线性内插
像素间的一些基本关系
邻域
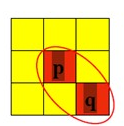
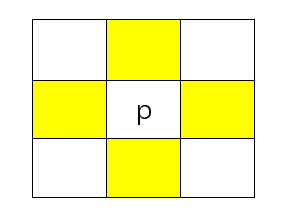
坐标(x,y)处的像素$p$有两个水平相邻像素和2个垂直的相邻像素,坐标为:
$$
(x+1,y),(x-1,y)(x,y+1),(x,y-1)
$$
这组像素称为$p$的 4邻域用 $N_4(p)$来表示。(黄色部分为邻域部分)
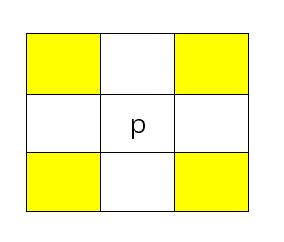
$p$的4个对角的相邻像素坐标为:
$$
(x+1,y+1),(x+1,y-1),(x-1,y+1),(x-1,y-1)
$$
用 $N_D(P)$来表示。(黄色部分为邻域部分)
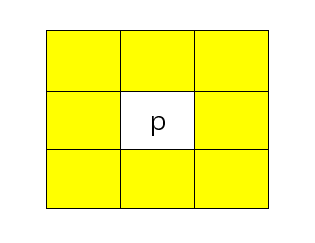
这些相邻像素和4邻域合称为$p$的8邻域,用 $N_8(P)$来表示。点$p$的相邻像素的图像位置集称为$p$的邻域。(黄色部分为邻域部分)
如果一个邻域包含$p$,那么称该邻域为闭邻域,否则称其为开邻域
邻接
令 $V$是用于定义邻接的灰度值集合。在二值图像中,指值为1的像素的邻接时, $V={1}$ 在灰度图像中,这一概念相同,但集合 $V$通常包含更多元素
4邻接
$q$在集合 $N_4(P)$中时,值在$V$中的两个像素 $p$和 $q$是4邻接的
8邻接
$q$在集合 $N_8(P)$中时,值在 $V$中的两个像素 $p$和 $q$时8邻接的
$m$邻接(混合邻接)
若 $q$在 $N_4(P)$中 或者 $q$在 $N_D(P)$中,且集合 $N_4(p) \bigcap N_4(q) $中没有值在 $V$中的像素,那么值在 $V$中的两个像素 $p$和 $q$是 $m$邻接的
目的:消除8邻接时可能导致的歧义性
邻接例子解释(不一定对,仅为自己所参考):
点我查看详情
若集合 $V$为 $V={1,2,3,4}$,点 $P=1$,则点 $P$的四邻域如下:
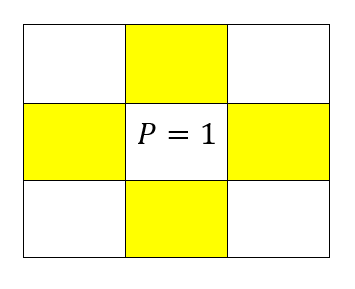
则黄色所示区域为点 $P=1$的4邻域,根据书中描述所示,若点 $q=2$,并且处于上图所示的黄色区域中,则称p、q是4连接的,例图如下(若点 $p$像素值为1,点 $q$像素值为2,并且点 $q$在点 $q$的右侧):
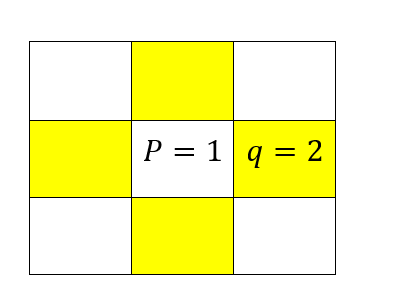
8邻接:
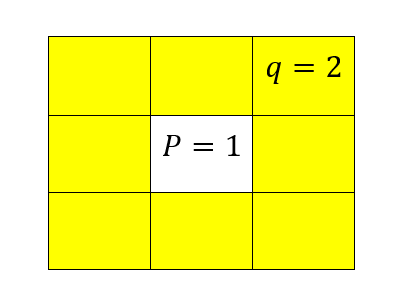
例图如下(黄色区域为点 $p$的8邻域区域;若点 $p$像素值为1,点 $q$像素值为2,并且点 $q$在点 $q$的右上侧):
混合邻接:
由描述可进行推导:定义集合 $V$ 为 $V={1,2}$,点 $p=1,q=1,r=2$,若点 $p$在点 $q$的8邻域中,并且且在集合 $N_4(p) \bigcap N_4(q) $中,没有 ${1、2}$这两个像素值,则说点 $p$和点 $q$是 m邻接的.
请注意:m邻接和前面的4邻接与8邻接并不冲突,p、q可以是4邻接的同时也是m邻接
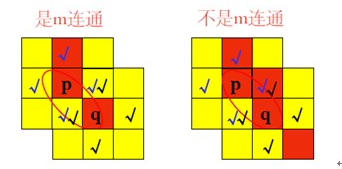
例图如下(例图原帖):
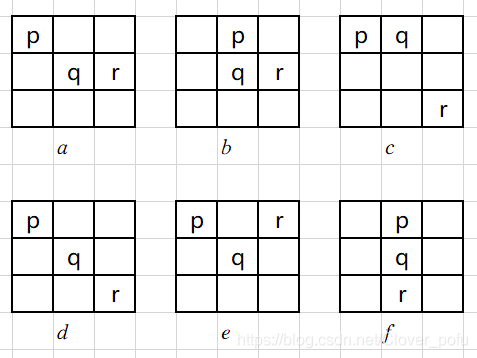
那么:
图(a)中,p和q是m邻接、8邻接的。q和r是m邻接、4邻接的。p和r不邻接。
图(b)中,p和q是m邻接、4邻接的。q和r是m邻接、4邻接的。p和r是8邻接、但不是m邻接的
(因为p和r的4邻域交集中,有个q是属于V的)。
图(c )中,p和q是m邻接、4邻接的。r没有和p或q邻接。
图(d)中,p和q是m邻接、8邻接的。q和r是m邻接、8邻接的。p和r不邻接。
图(e)中,p和q是m邻接、8邻接的。q和r是m邻接、8邻接的。p和r不邻接。
图(f)中,p和q是m邻接、4邻接的。q和r是m邻接、4邻接的。p和r不邻接。
连通 (部分内容参考博文)
令 $S$表示图像中像素的一个子集。如果完全由 $S$中的所有像素组成的两个像素 $p$和 $q$之间存在一个通路,那么称 $p$和 $q$在 $S$中是连通的。
连通分量
对于 $S$中的任何像素 $p$,在 $S$中连通到该像素的像素集称为 $S$的连通分量
连通集
若 $S$只有一个连通分量,则集合 $S$称为连通集
4连通
对于具有值$V$的像素$p$和$q$,如果$q$在集合$N_4(p)$中,则称这两个像素是4连通的
8连通
对于具有值$V$的像素$p$和$q$,如果$q$在集合$N_8(p)$中,则称这两个像素是8连通的
m连通
若 $q$在 $N_4(P)$中 或者 $q$在 $N_D(P)$中,且集合 $N_4(p) \bigcap N_4(q) $中没有值在 $V$中的像素,则称两个像素是m连通的
区域&边界
若集合 $R$是一个连通集,则称 $R$为图像上的一个区域。
两个区域 $R_i$和 $R_j$联合形成一个连通集时,称$R_i$和 $R_j$为邻接区域。
不邻接的区域称为不相交区域
注意:为了使定义有意义,因此在使用过程中需要指定邻接的类型
距离测度
对于坐标为 $p(x,y),q(u,v),s(w,z)$的三个像素点,如果
- $D(p,q)\geq0$ 【若出现 $D(p,q)=0$则当前仅当 $p=q$】
- $D(p,q)=D(q,p)$
- $D(p,s)\leq D(p,q)+D(q,s)$
则 $D$是一个距离函数或者是距离测度。
- 欧几里得距离($D_e$)
$p$和 $q$之间的欧几里得距离定义为
$$
D_e(p,q)=\sqrt{(x-u)^2+(y-u)^2}
$$
对于这个距离测度,到点 $(x,y)$的距离小于等于 $r$的像素,是中心在 $(x,y)$,半径为 $r$的圆盘
- 城市街区距离( $D_4$)
$p$和 $q$之间的距离 $D_4$(城市街区距离)定义为
$$
D_4(p,q)=|x-u|+|y-v|
$$
此时,到 $(x,y)$的距离 $D_4$小于等于 $d$的像素形成的一个中心为 $(x,y)$的菱形.
例如到 $(x,y)$的距离$D_4$小于等于2的像素形成如下恒定距离的轮廓:
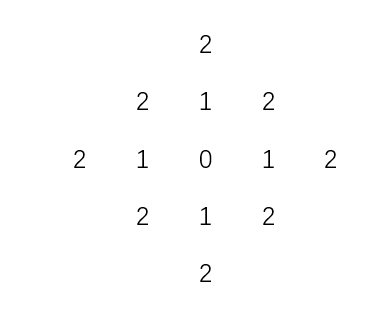
其中, $D_4=1$的像素是 $(x,y)$的4邻域.
棋盘距离($D_8$)
定义为:
$$
D_8(p,q)=max(|x-u|,|y-v|)
$$
此时,到 $(x,y)$的距离 $D_8$小于等于 $d$的像素形成一个中心为 $(x,y)$的方形.例如到中心点的距离 $D_8$小于等于2的像素形成如下恒定距离的轮廓: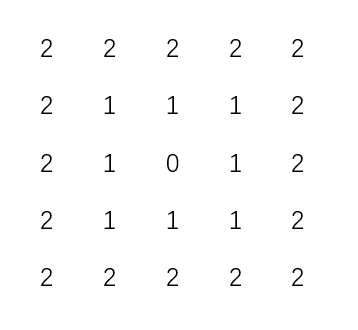
其中 $D_8=1$的像素是位于点 $(x,y)$的像素的8邻域.
数学工具
对应元素运算和矩阵运算
图像可以等效地视为矩阵。两幅图像的阵列相乘是图像矩阵的点乘;矩阵相乘是两个图像矩阵的相乘。
矩阵运算
以 $\begin{bmatrix} a_{11} & a_{12}\a_{21} & a_{22} \end{bmatrix}$与 $\begin{bmatrix} b_{11} & b_{12}\b_{21} & b_{22} \end{bmatrix}$作为图像(矩阵)为例:
两幅图像对应元素的积(用符号 $\otimes$或者 $\odot$ 表示):
$$
\begin{bmatrix} a_{11} & a_{12}\a_{21} & a_{22} \end{bmatrix} \otimes \begin{bmatrix} b_{11} & b_{12}\b_{21} & b_{22} \end{bmatrix} = \begin{bmatrix} a_{11}b_{11} & a_{12}b_{12} \ a_{21}b_{21} & a_{22}b_{22} \end{bmatrix}
$$
因此,对应元素的积是由一对对应像素相乘得到的。图像的矩阵乘积使用如下的矩阵乘法规则得到的:
$$
\begin{bmatrix} a_{11} & a_{12}\a_{21} & a_{22} \end{bmatrix} \begin{bmatrix} b_{11} & b_{12}\b_{21} & b_{22} \end{bmatrix} = \begin{bmatrix} a_{11}b_{11}+a_{12}b_{21} & a_{11}b_{12}+a_{12}b_{22} \ a_{21}b_{11}+a_{22}b_{21} & a_{21}b_{12}+a_{22}b_{22} \end{bmatrix}
$$
线性运算和非线性运算
考虑一般算子 $\H$ ,该算子对给定的一幅输入图像 $f(x,y)$ 产生一幅输出图像 $g(x,y)$:
$$
\digamma[af_1(x,y)+bf_2(x,y)] = a\digamma[f_1(x,y)]+b\digamma[f_2(x,y)] = ag_1(x,y)+bg_2(x,y)
$$
则称算子 $\H$是一个线性算子。
加性
两个输入求和的线性运算的输出,与分别对应输入进行运算并求和得到的结果相同
同质性
输入乘以常数的先行原酸的输出,与原始输入乘以该常数的运算的输出相同
对于不满足上式的运算式称为非线性运算。
算术运算
图像间的算术操作是阵列操作,在相应像素对之间执行加减乘除。
应用:
- 图像相加(平均)降低噪声
- 图像相减比较图像
集合运算与逻辑运算
空间运算
单像素运算
数字图像处理中最简单的运算,使用变换函数 $T$ $s= T(z)$来改变图像中各个像素的灰度。
$z$是原图像的灰度值, $s$是处理后的图像对应部分的像素值
邻域运算
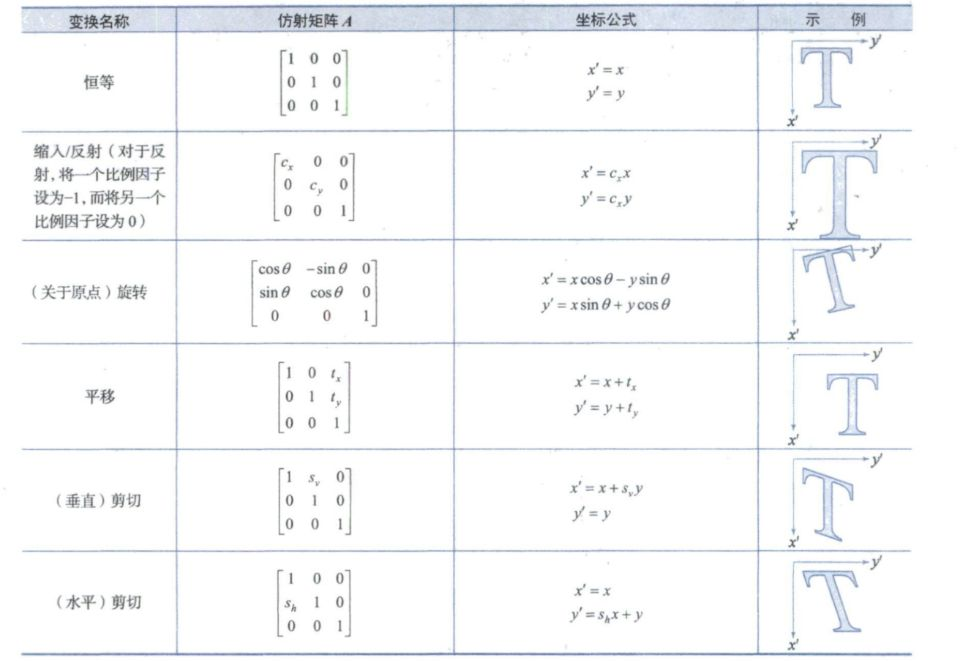
几何空间变换(橡皮膜变换,坐标空间变换+灰度内插)
仿射变换:对一组坐标点做尺度,旋转,平移或偏移
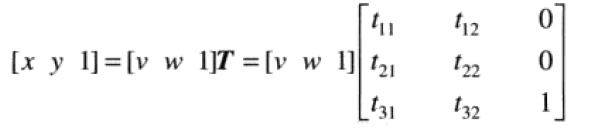
仿射变换图如下: