图像复原与重建
请注意:文章中的[^123]标码,代表数字图像处理——冈萨雷斯版图书的指定页码部分
复原与重建相关关系
图像增强主要为主观处理,图像复原很大程度为客观处理
图像复原是利用退化现象的先验知识来复原已经退化的图像,因此主要是对退化建模并且应用逆过程来复原图像
图像退化/复原的一个模型
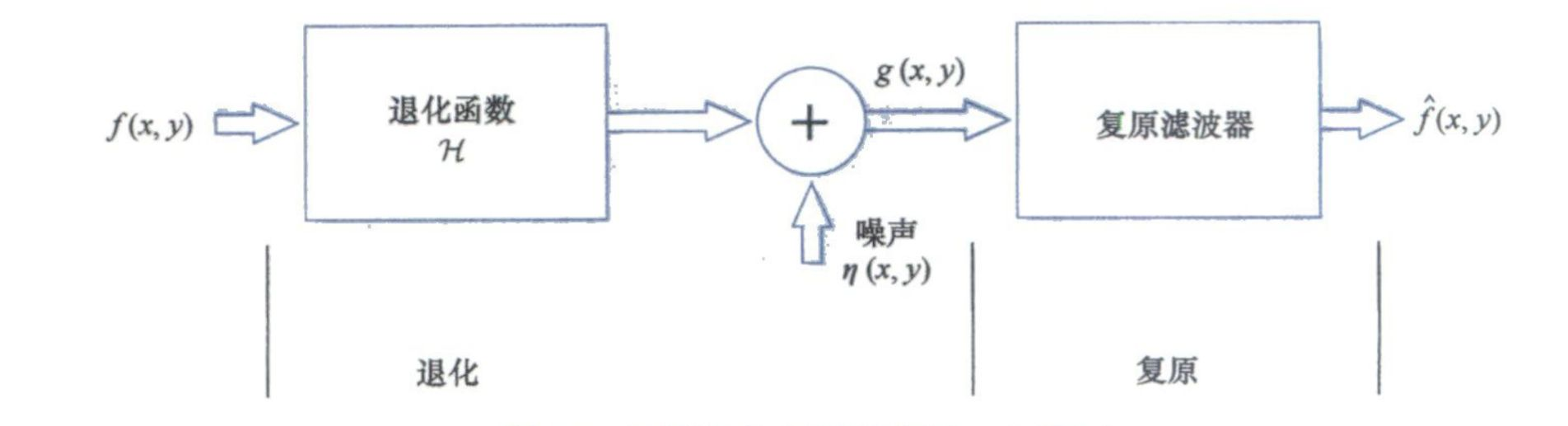
常见的复原算法
只存在噪声的复原——空间滤波
均值滤波器
算术平均滤波器[^227]
使用大小$m*n$的一个空间核来实现,核的所有系数都是 $1/mn$均值滤波平滑图像中的局部变化,会降低图像中的噪声,但会模糊图像
几何均值滤波器[^227]
几何均值滤波器实现的平滑可与算数平均滤波器相比,但损失的图像细节会更少
谐波平均滤波器
其滤波器既能处理盐粒噪声,又能处理类似于高斯噪声的其他噪声,但是不能处理胡椒噪声
反谐波平均滤波器[^227]
适用于降低或消除椒盐噪声,$Q$为正值时可以消除胡椒噪声,$Q$为负值时,可以消除椒盐噪声,但是
不可以同时消除以上两种噪声
$Q=0$时,反谐波平均滤波器简化为算术平均滤波器
$Q=-1$时,简化为谐波平均滤波器
统计排序滤波器
统计排序滤波器为空间滤波器,基于滤波器所围邻域中的像素值的顺序,结果决定了滤波器的响应。
中值滤波器[^229]
使用预定义的像素邻域的灰度中值来代替像素的值
可以有效的降低某些随机噪声,并且模糊度要小得多,对于单极或双极冲激噪声,中值滤波器效果更好
最大值滤波器和最小值滤波器[^230]
最常使用的统计排序滤波器,但不是唯一使用的滤波器。
最大值滤波器可以找到图像中的最亮点或者用于削弱与明亮区域相邻的暗色区域
最大值滤波器可以降低胡椒噪声;
最小值滤波器可以找到图像中最暗点,或者用于削弱与暗色区域相邻的明亮区域
可以降低椒盐噪声
中点滤波器[^230]
统计排序滤波器和平均滤波器的结合,最适合用于处理随机分布的噪声,如:高斯噪声、均匀噪声
修正阿尔法均值滤波器[^230]
适合处理多种混合噪声,如高斯噪声和椒盐噪声
自适应滤波器
自适应滤波器的性能要优于前面讨论的所有滤波器,但增大了其复杂度
自适应局部降噪滤波器[^233]
均值为计算平均值区域上的平均灰度
方差是该区域上的图像对比度
自适应中值滤波器[^234]
若椒盐噪声的空间密度较低,则使用中值滤波器滤波效果性能更好。
自适应中值滤波器可以处理更大概率的噪声
优点:可以在保留图像细节的同时平滑非冲激噪声
使用频率域滤波器降低周期噪声
频率域技术可以有效分析并滤除周期噪声
陷波滤波深入介绍[^236]
最优陷波滤波[^239]
线性位置不变退化[^243]
估计退化函数
估计图像复原中退化函数主要有三种:
- 观察法
- 试验法
- 数学建模法
采取观察法估计退化函数[^245]
应用:复原一幅具有历史价值的老照片
采取试验法估计退化函数[^245]
采用建模法估计退化函数[^245]
逆滤波
直接逆滤波的性能一般较差,一般改进之后进行运算
最小均方误差(维纳)滤波
此算法基础:将图像和噪声视为随机变量